Article Content

What are the musical possibilities of a rectangle? Four sides and four equal angles imply symmetry in form but also divisibility and commonality.

• 4/4 meter
• 4 sections
• 4 bars
• 4 repetitions
• 4 + 4 = 8 Bars
• 8 + 8 = 16 Bars

The angles are 90º each. Creating summed variations we get:

• 90
• 90 + 90 = 180
• 90 + 90 +90 = 270
• 90 + 90 + 90 + 90 = 360

Thinking about angles and degrees brings to mind the concept of phase and phase-related effects in audio such as phase modulation and phase distortion synthesis.

Quantizing to an equal-tempered scale:

• 90 Hz is closest to F#1
• 180 Hz is closest to F#2
• 270 Hz is closest to C#3
• 360 Hz is closet to F#3

Thinking microtonally:

• 90 Hz = F#2 minus 47 cents
• 180 Hz = F#3 minus 47 cents
• 270 Hz = C#4 minus 45 cents
• 360 Hz = F#4 minus 47 cents
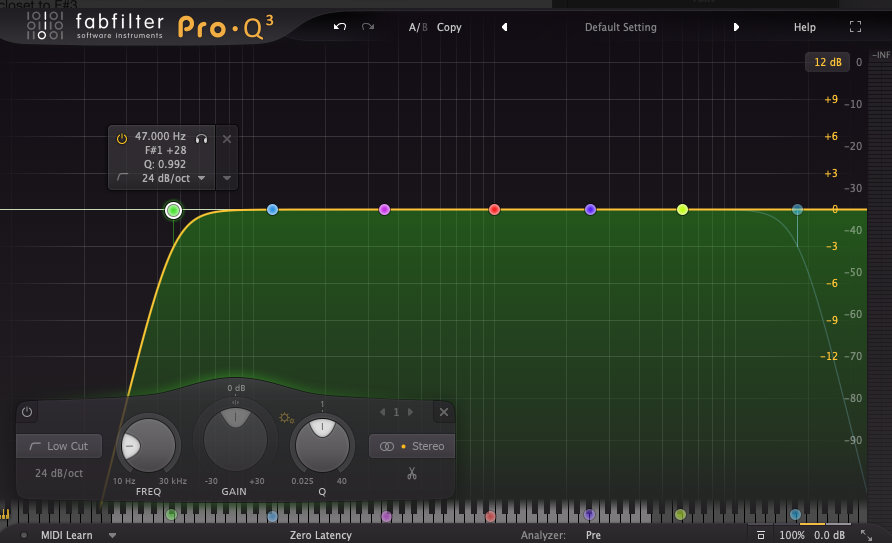
• 47 Hz = F#0 plus 28 cents
• 45 Hz = F#0 minus 47 cents
• 28 Hz = A-1 plus 31 cents
• 31 Hz = B-1 plus 7 cents
• 7 Hz is below the audible, but it’s a useable LFO rate

Side note: there are 100 cents in every 1/2 step.

Thinking in terms of harmony:

• F# A B C# = F#min (add4)

Selected scales containing these notes include:

• F# aeolian mode (natural minor)
• F# dorian mode
• F# phrygian mode
• F# harmonic minor (+ all associated modes)
• F# melodic minor (+ all associated modes)
• A major (+ all associated modes)
• E major (+ all associated modes)
• D major (+ all associated modes)

The frequencies mentioned above could be used as parameter settings in a filter or EQ:

• Cut-off frequencies (LP, HP, BP, BR)
• Center frequencies (Bell, Notch)
• Slope or Q

The 4 sides of a rectangle bring to mind a 4 stage envelope. Parallel sides are equal and there are 2 short sides and 2 long sides.

ADSR = attack/decay/sustain/release

Possibilites:

• Attack time = decay time
• Attack time = release time
• Release time = decay time
• Sustain level = 1/4 attenuation in level after the decay stage = .75 based on a normalized amplitude (0 dB = 1.0)

Thinking about wavelengths (using 1132 ft/second and 344 meters/second as the speed of sound) we get:

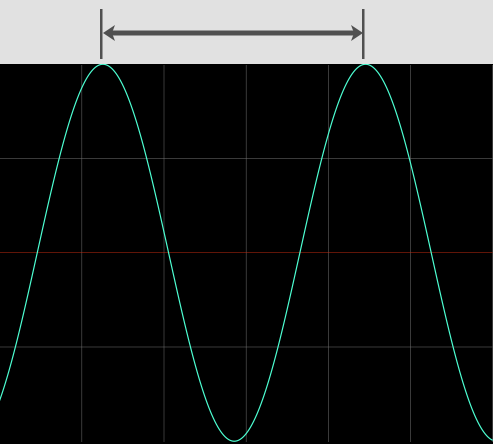
• 90 Hz = 12.58 feet = 3.82 meters
• 180 Hz = 6.29 feet = 1.91 meters
• 270 Hz = 4.19 feet = 1.27 meters
• 360 Hz = 3.14 feet = .96 meters

It’s fascinating that the wavelength of 360 Hz using the speed of sound at 1132 ft/second comes close to pi = 3.14159265359 (in feet).

The quantities above could be used for:

• LFO rates
• Reverb time (milliseconds or seconds)
• Delay time (milliseconds or seconds)
• Envelope times (milliseconds or seconds)
• Compression parameter settings
• Detuning settings

Think about waveforms — a rectangular wave is nothing more than a square waveform with an altered pulse width setting.

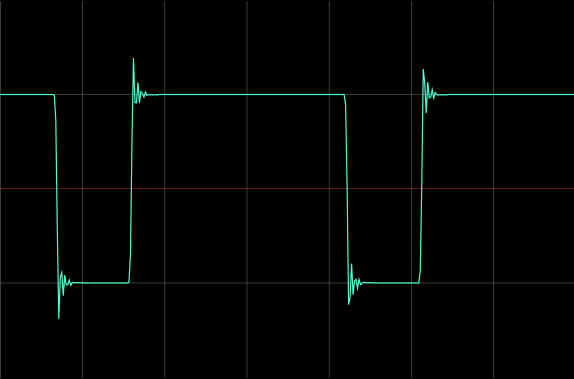
Continually changing the pulse width is called pulse width modulation (PWM) and is an iconic sound in synthesis.

The rectangular waveform could be:

• One of the main oscillators in a subtractive synth
• A carrier or modulating oscillator in an FM synth
• An LFO waveform shape used to modulate any parameter

Getting back to the “four-ness” of the shape, consider:

• The 4th preset
• 4 LFO’s
• 4 Envelopes
• 4 Oscillators
• 4 Instruments
• 4 Layers
• 4 Parts
• 4 Inserts
• 4 Sends
• 4 Tracks
• 4 Sections
• 4 Automated Parameters
• 4 Note chords
• 4 Rhythmic Divisions
• 4 Step Sequencers
• 4 Octaves
• 4 Note melody
• 4 Chord Progression
• 4 Pole Filter = 24 dB Slope
• 4 Verses
• 4 Choruses

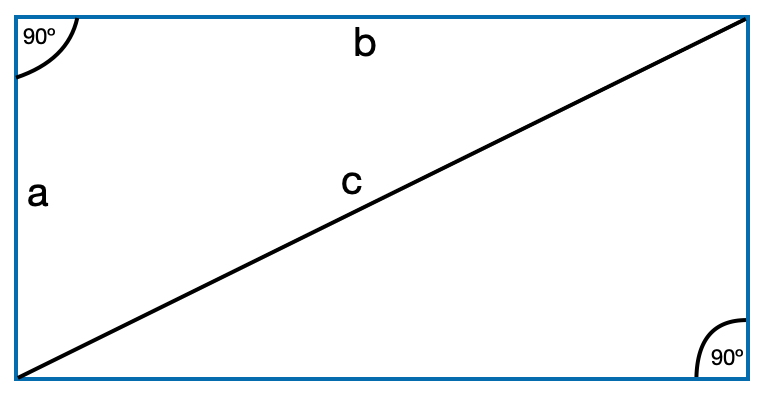
A rectangle divided in half from opposite corners results in two right triangles and brings to mind the Pythagorean Theorem (a² + b² = c²). Said another way, the sum of the squared values of the two short sides equals the squared value of the long side or the hypotenuse. Thinking of Pythagorus ( c. 570 – c. 495 BC) brings to mind the harmonic series and also Pythagorean tuning systems. Based on a 12-tone Pythagorean scale built on an F# root, we get the following detuning setup from Logic Pro’s alternate tuning parameters.

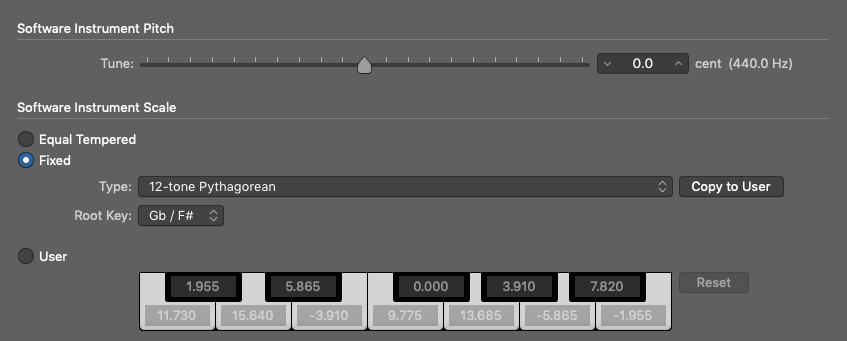
Also from the paragraph above we can abstract additional notes:

• • C note (from a² + b² = c²)
  • 570 Hz = C#4 plus 48 cents (birth of Pythagorus)
  • 495 Hz = B3 plus 4 cents (death of Pythagorus)

A rectangle is comprised of 4 connected lines. If we start at one point and follow the line you return to the beginning – a sort of recapitulation:

• 4 melodic lines
• 2 long lines
• 2 short lines

Thinking about harmonic rhythm:

• 4 chord pattern
• 2 chord pattern
• 2 beats per chord
• 4 beats per chord

Returning to the value of 90º, consider:

• 90 bars
• 90 seconds
• 90 beats
• 180 bars
• 180 seconds
• 180 beats
• etc.

So What’s the Point?

By this time (if you’ve gotten this far), you might be thinking — what’s the point? The point is there doesn’t have to be a point. Music doesn’t have to be about expressing emotions or feelings unless that’s what you want it to do. It doesn’t need to follow the rules of Western harmony to sound “good.” And it definitely doesn’t need to be “correct” in any quantifiable way.

The rules of counterpoint and voice leading were developed by composers and theorists that strove to maintain and codify a certain aesthetic. People like Heinrich Schenker (1868-1935) theorized that there was an underlying structure that could not only be used to explain the coherence of a musical work, but that rules could be extrapolated and used as a sort of structural template to create new work that was equally coherent and “successful.”

Many would argue that this approach works fine. There is no doubt that the smoothness achieved by using common practice voice leading constructs, like the avoidance of parallel 5ths and octaves, have become familiar to our ears and can be found in all sorts of genres. While Arnold Schoenberg (one of the developers of dodecaphonic or 12-tone harmony) strove to extend the Romantic tonal relationships of the 19th Century towards an atonal aesthetic, he did not completely abandon all the rules that had been established to that point.

John Cage, the contemporary American composer known for his prepared piano pieces, the so-called “silence” piece 4’33” and the use of indeterminacy in music creation, relates a story when he was a student of Schoenberg. As I mentioned in a previous article:

“As a young composer [Cage] studied counterpoint with Arnold Schoenberg who would often ask his students to provide every possible voice leading solution for a given melody. He would then ask, “What is the principle underlying all of the solutions?” It wasn’t until years later that Cage realized that what all the solutions had in common was the question!”

That relevance of the question is crucial since every work of art starts with not just one, but a series of questions. In terms of new piece of music you might ask:

• What will be the instrumentation?
• What will be the underlying harmonic relationships?
• What will be the rhythmic content?
• What will be the tempo?
• etc.

If the answers to the questions are the same every time, you can see how redundancy might eventually become an issue. Likewise, if the same questions themselves are asked over and over again, your choices might become habitual and routine.

I used the process of abstracting musical constructs from a rectangle to suggest that musical ideas are everywhere around us. Not just in terms of direct sound sources like field recordings and found sounds, but in terms of numerology, visual and geometric proportionality, mathematics, physics, philosophy – literally everywhere.

Ready to elevate your ears?

It doesn’t have to take years to train your ears.

Get started today — and you’ll be amazed at how quickly using Quiztones for just a few minutes a day will improve your mixes, recordings, and productions!

Download for iOS Download for Mac

However, the underlying constructs of a musical work are far less important than the end result. To doggedly use a pre-devised methodology to dictate your choices throughout the composing process without allowing your ear and intuition to intervene or adjust the choices that emerge from the system would be nothing more than an exercise in stubborn rationality, divorced from the creative impulse. To use a cliché – rules are meant to be broken. This especially holds true for the rules you invent yourself.

The average listener doesn’t care what scale you’re using or what the rate of an LFO is. And they couldn’t care less if you based some shitty track on a rectangle. But if it moves them emotionally or engages them intellectually or both, you have a “successful piece.” For composers and producers, the impetus to write and the motivation to simply start can sometimes be elusive. If you can derive so many musical ideas from a simple rectangle, there must be a treasure trove of ideas in the very place where you’re reading this article.

Check out my other articles, reviews and interviews

Follow me on Twitter / Instagram / YouTube

Philip Mantione

Philip Mantione is a composer, synthesist, guitarist, educator and sound artist active in the LA experimental music scene. His music has been presented in festivals, museums and galleries worldwide. His current project is TriAngular Bent, an electroacoustic trio featuring Don Preston (founding member of Frank Zappa’s Mothers of Invention) and circuit bending virtuoso, Jeff Boynton. Details at philipmantione.com