The Fundamentals of Subtractive Synthesis
10/26/2018
Article Content
In past articles, I have provided overviews of several types of synthesis techniques including:
- The Fundamentals of AM Synthesis
- The Basics of Wavetable Synthesis
- The Basics of Additive Synthesis
- Introduction to Granular Synthesis
- Introduction to FM Synthesis
Another approach, which is perhaps the most prevalent, is Subtractive Synthesis, described by Creasey as an approach in which, “…filtering is the principle tonal modification technique…” (Creasey 502). Of course, many other synthesis models use filtering to some extent, but in subtractive synths, the sources to be filtered are generally simple waveforms (eg. sine, triangle, rectangle, etc.), or noise generators. A distinct benefit of this technique in the digital realm is the possibility of creating complex timbres with relatively low CPU load as compared to additive synthesis or other methods.
In the most basic case, subtractive synthesis involves a sound source (oscillating waveform or noise), an audio filter and an amplification section. Each of these stages can be modified through some sort of modulation process. The block diagram from the Logic Instrument Manual below provides a succinct visualization of the method.
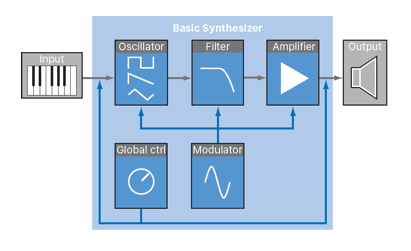
There is typically some method of input (often a MIDI controller) which provides pitch, velocity and durational information to the system. Playing a note activates an amplitude envelope, controls the frequency of the oscillator and may activate other processes as well. Global controls can include pitch bend settings, transposition or glide (portamento) settings.
Sound Sources
Basic waveforms such as square, triangle, sawtooth, etc. are the most common sources used in Subtractive Synthesis.
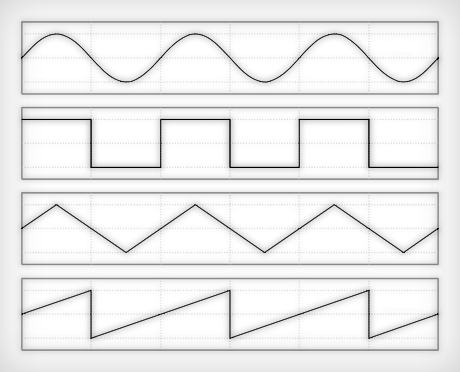
(image source)
Geometrically perfect waveforms in the digital realm, “… contain an infinite number of frequency components … which can cause nasty problems … since an audio interface cannot reproduce frequencies above half its sampling rate.” (Cipriani 299) This is referred to as the Nyquist frequency; where half the sampling rate frequency is the highest alias-free signal that can be reproduced. (Roads 30) Thus a system using a 48 kHz sampling rate can accurately reproduce frequencies up to 24 kHz. Attempts to reproduce frequencies above this range will result in undesired and typically non-harmonic components. Band-limited oscillators are used in digital systems because they are designed so that their component frequencies never rise above half the sampling rate. (Cipriani 299)
Noise Generators are rich sources of sound and provide percussive angularity to sounds when short amplitude envelopes are used. Two common flavors are white and pink noise.
White Noise contains all audible frequencies with random amplitudes.
Pink Noise also contains all audible frequencies, but they are attenuated by 3 dB per octave as you move up the spectrum.
Filter Basics
Filtering is a complex subject deserving of an article (or book) all its own, but below is a list of the basic shapes you may encounter and the parameters you should be aware of.
Filter Types
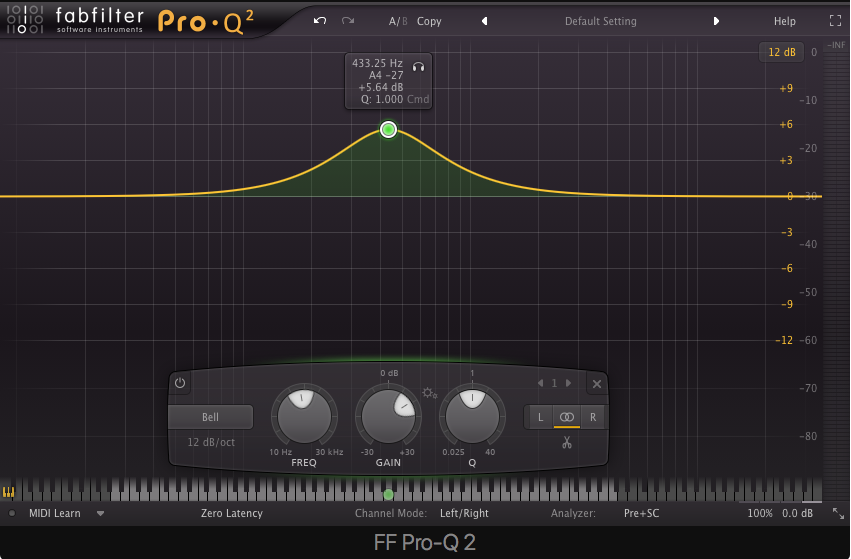
Bell – allows frequencies to be attenuated or boosted around a center frequency.
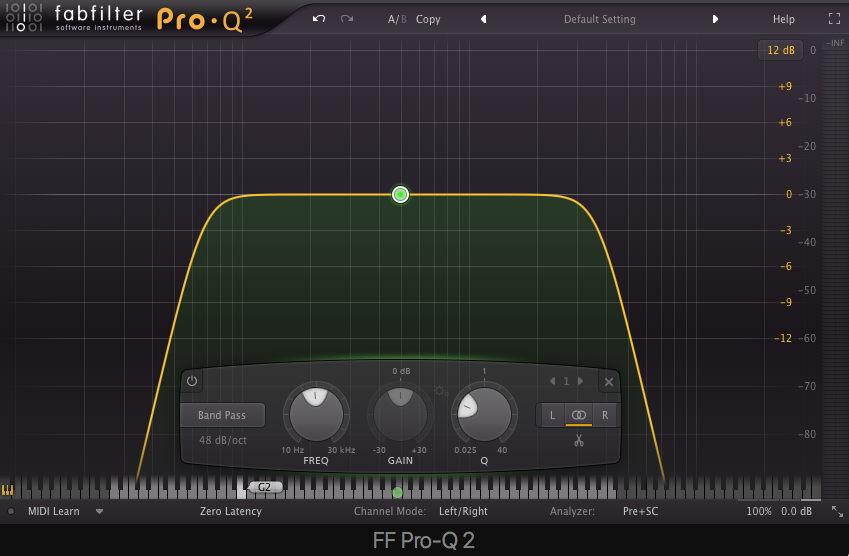
Bandpass – allows frequencies to pass between low and high cutoff frequencies.
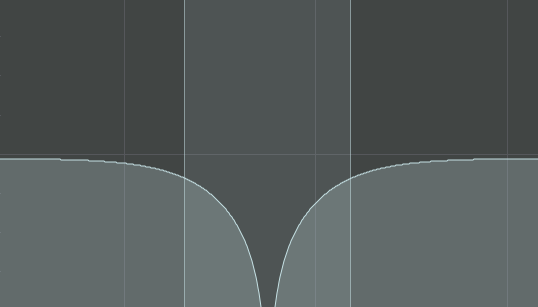
Band Reject or Band Stop – allows frequencies to pass above or below high or low cutoff frequencies, respectively.
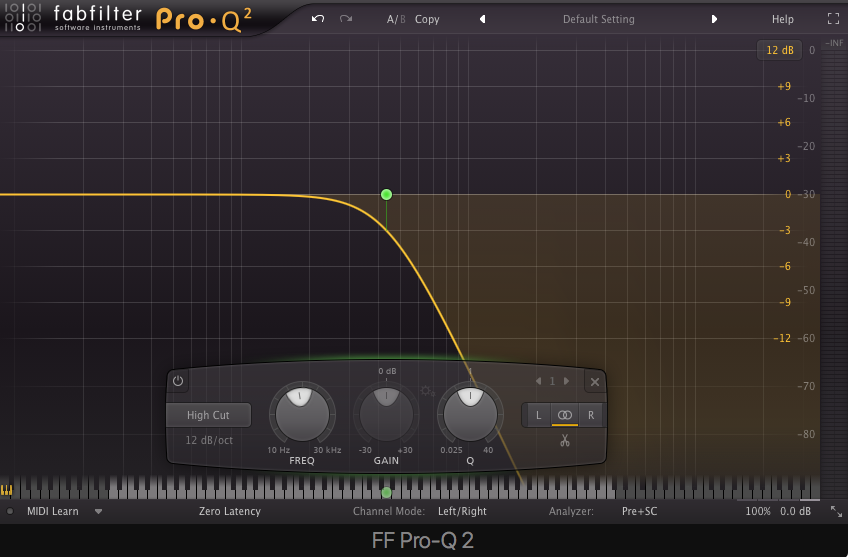
Low-Pass (or High Cut) – allow frequencies to pass below a cutoff frequency.
High-Pass (or Low Cut) – allow frequencies to pass above a cutoff frequency.
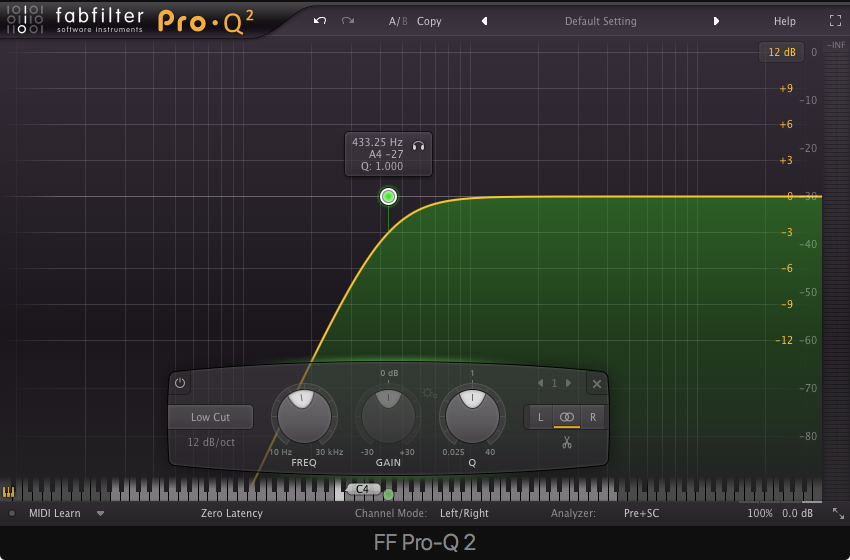
High Shelf – attenuates or boosts frequencies above a cutoff frequency.
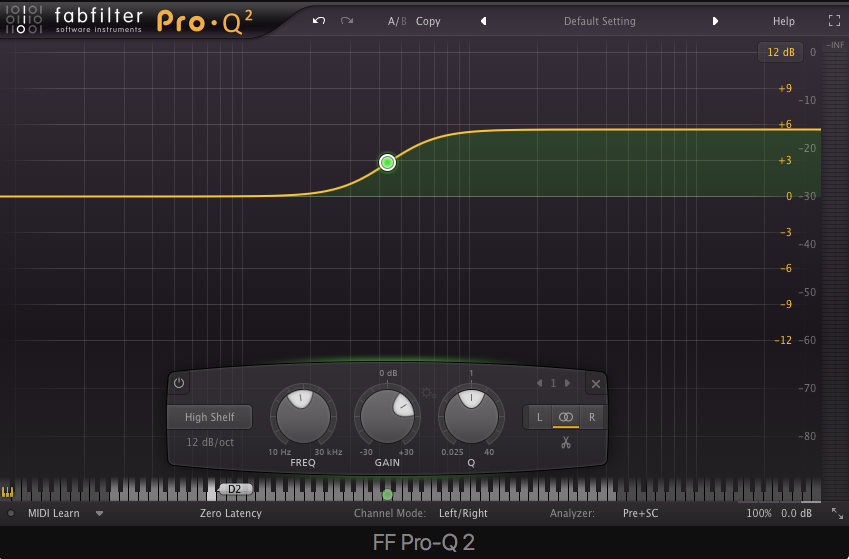
Low Shelf – attenuates or boosts frequencies below a cutoff frequency.
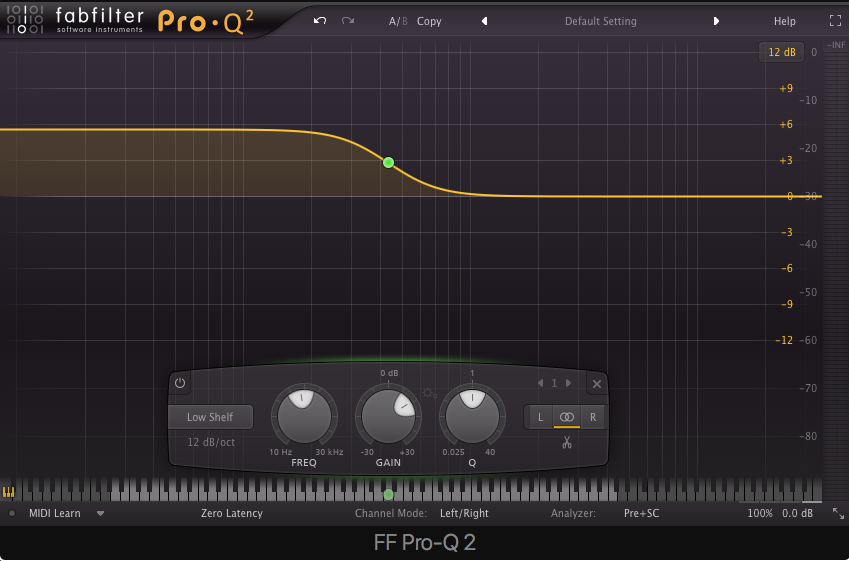
Tilt Shelf – as frequencies above a center frequency are attenuated, a corresponding boost is applied to frequencies below the center frequency and vice versa.
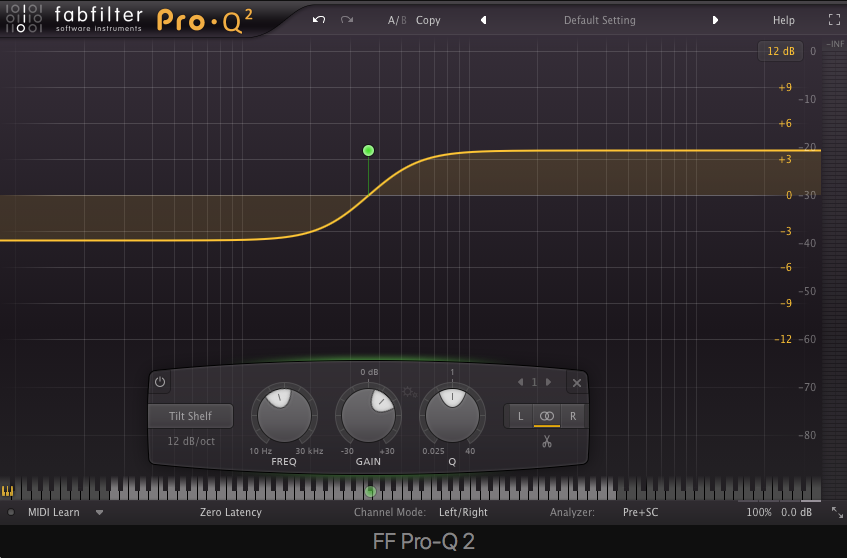
Resonant Bandpass – similar to a bandpass filter but allows for a center frequency to be boosted and self-resonate.
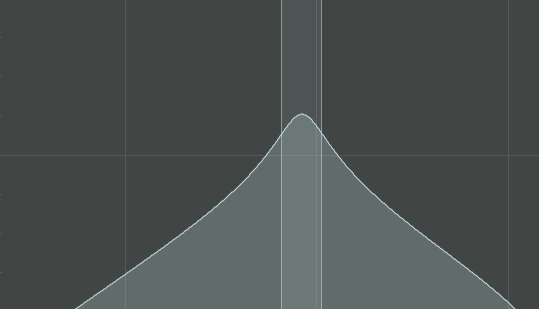
Notch – similar to a bell filter with an extremely high Q setting, creating a very narrow bandwidth for attenuation or boosting.
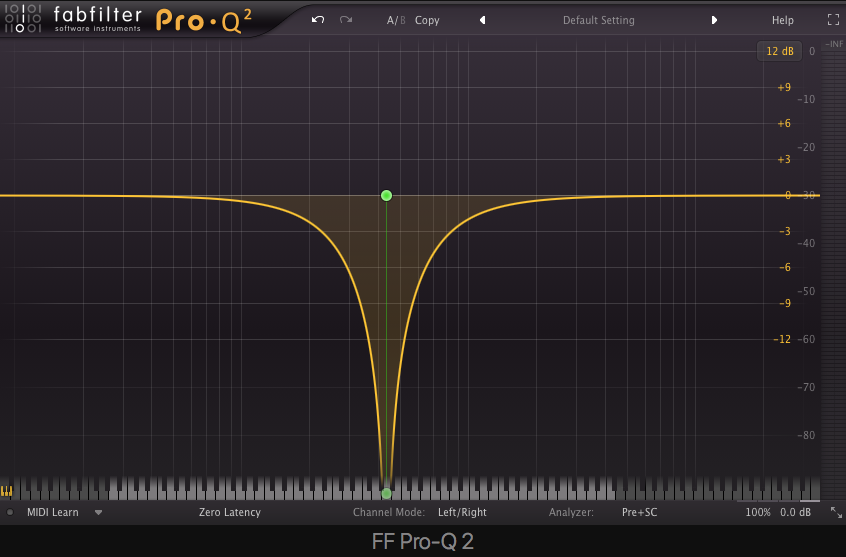
All-Pass – filters alter the phase of the input signal and are often used for creating algorithmic reverbs.
Filter Parameters
- Gain – increases or reduces gain at the indicated frequency
- Center Frequency – the frequency at which attenuation of accentuation begins (above and below)
- Cutoff Frequency – the frequency at which attenuation of accentuation begins (above or below depending on the type of filter).
(NOTE: there is always a transition period around the center or cutoff frequency)
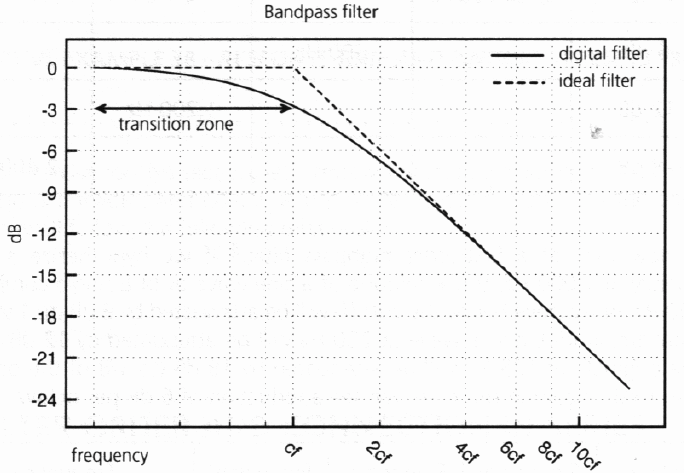
- Q – this determines the bandwidth around a center frequency. The higher the Q, the more narrow the bandwidth and vice versa. With IIR (Infinite Impulse Response) filters, increasing the slope will cause a boost at the cutoff frequency to the point where it can be made to self-oscillate.
- Slope – usually measured in terms of attenuation per octave above or below a cutoff frequency. (Example: a slope setting of 12 dB applied to a low-pass filter with a cutoff frequency of 500 Hz, means that there will be a 12 dB attenuation of the signal at 1000 Hz (or one octave above the cutoff).
Amplifier Section
The last stage of a subtractive synthesis (and most synths) is the amplifier section. Here envelopes can be used to shape the final output. Traditional envelope stages are attack, decay, sustain and release (ADSR). But more complex envelopes are also common and can include multi-segment processing, looping functionality, syncing capability or dynamic parameters.
Check out my article on envelopes for more information: The Basics of Synth Envelope Parameters, Functions and Uses
Ready to elevate your ears?
It doesn’t have to take years to train your ears.
Get started today — and you’ll be amazed at how quickly using Quiztones for just a few minutes a day will improve your mixes, recordings, and productions!
In addition to modulating amplitude, the output of envelope data can typically be routed to many other parameters in the signal path, allowing the user to sculpt the timbral and percussive qualities of the resulting sound as it unfolds over time. Velocity can be set to influence the effect of an envelope in order to take advantage of performance data in real time or by applying randomization or continuous controller performance data in the MIDI editing and/or automation process.
Output sections also very often include distortion or saturation effects, chorusing, delay, reverb and spatialization processes. (It should be noted that some synths also include drive or saturation effects before or directly after the filtering process).
Modulation Section
Low-frequency oscillators (LFO’s) are an extremely common method of modulating any number of parameters in a subtractive synthesis process. And as discussed above, envelope generators are equally powerful as sources of modulation and can be performance controlled to great effect. Since I’ve written extensively about these things in the past, you may want to check out the following articles:
Favorite Subtractive Synths
Subtractive synths come in all sorts of flavors and hybrid combinations in which other sorts of synthesis models are combined as part of the overall approach. Many use irregular wavetable shapes or those based on the timbre of acoustic instruments instead of basic sine, triangle, rectangular or sawtooth waves in the oscillator source section. They may have extremely sophisticated filter and modulation possibilities to shape the sound or wavetable synthesis approaches that scan through waveforms to create evolving and morphing oscillators. Below are a few of my favorite instruments that have a subtractive approach at the heart of their sound generation.
Twin 3 by Fabfilter
Thorn by Dmitry Sches
kHs One by Kilohearts
Model 15 by Moog
bx_oberhausen by Brainworx
Knifonium by Knif Audio
Lion by Unfiltered Audio
Predator 2 by Rob Papen
Zebra 2 by U-he
Vital by Matt Tytel
Serum by Xfer Records
Summation
You will find elements of subtractive synthesis in many software and hardware synthesizers regardless of the primary method of synthesis being employed. What makes the approach so attractive is the wide range of sonorities possible with just a few simple oscillators, a filter and an envelope. But don’t be fooled by this apparent lack of sophistication. Behind every simple approach to synthesis are countless engineers, developers and musicians determined to complexify and bastardize the process for their own demonic ends — and that’s where the real fun begins.
Sources
Cann, Simon. Becoming a Synthesizer Wizard: from Presets to Power User. Course Technology, 2010.
Cipriani, Alessandro, and Maurizio Giri. Electronic Music and Sound Design Theory and Practice with Max/MSP. ConTempoNet, 2013.
Creasey, D. J. Audio Processes: Musical Analysis, Modification, Synthesis, and Control. Routledge, 2017.
Roads, Curtis. The Computer Music Tutorial. MIT Press, 2012.
Russ, Martin. Sound Synthesis and Sampling. Focal Press, 2013.
Check out my other articles, reviews and interviews
Follow me on Twitter / Instagram / YouTube
Eleveate Your Ears
