The Basics of Additive Synthesis
Article Content
Additive Synthesis is considered the oldest form of sound synthesis dating back to its application in pipe organs. By controlling the routing of air through various pipes it’s possible to create a variety of timbres. “Additive Synthesis is a class of sound synthesis techniques based on the summation of elementary waveforms to create a more complex waveform.” (Roads, 2012, p. 134)
Although in theory any waveforms can be used, sine waves, the only pure waveforms without harmonics, are used most commonly. By summing several sine waves of varying frequency, amplitude and phase, we can create more complex sonorities. The use of sine waves make the process highly predictable and controllable.
For example, it’s possible to build a square wave by adding a series of sine waves together that are related in a very specific way. Starting with the fundamental frequency, odd harmonics are added that decrease in amplitude proportional to the harmonic number.
So if we start at 100Hz at a normalized amplitude of 1.0, the next tone would be 300Hz at an amplitude of .33 (or 1/3). Next would be the 5th harmonic tone at 500Hz at an amplitude of .2 (or 1/5). The more odd harmonics added using the same proportional amplitude adjustment, the more distinct the square wave becomes. Notice how the waveforms below change as more harmonics are added:
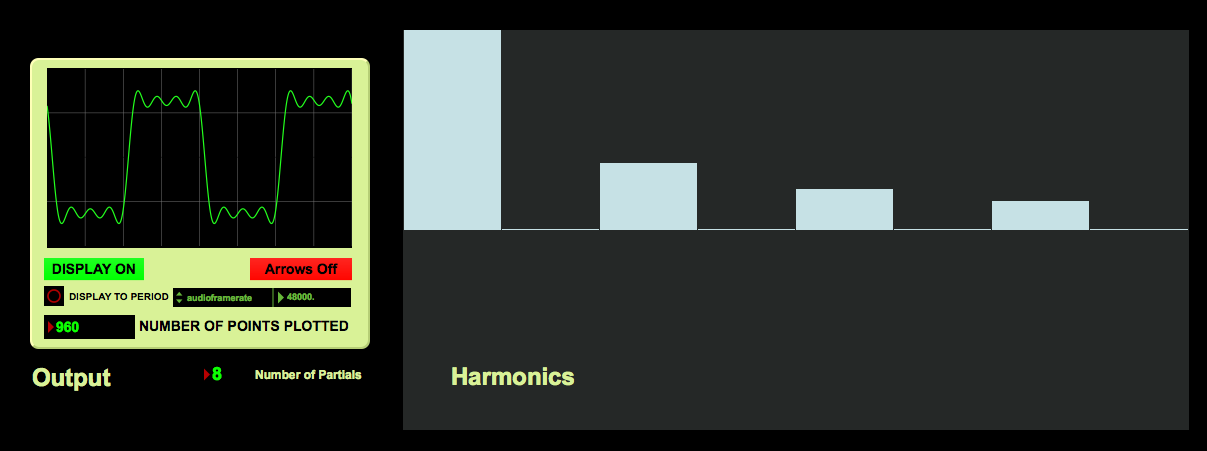
8 Harmonics
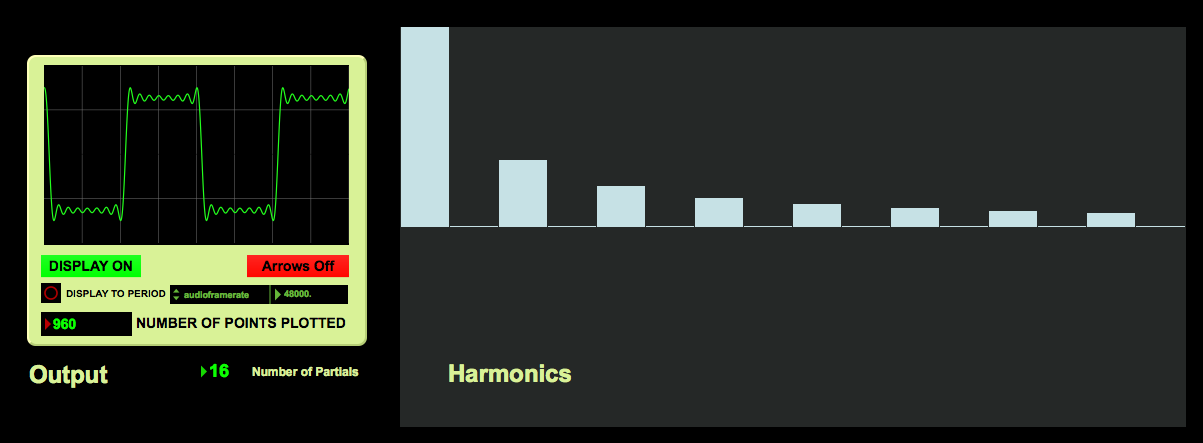
16 Harmonics
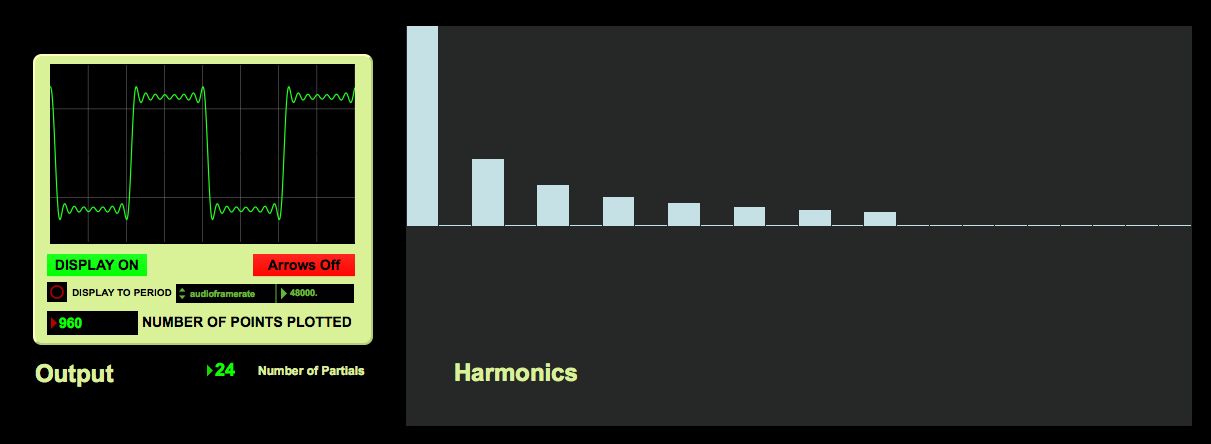
24 Harmonics
Again, the more harmonics used, the more distinct the resulting shape and sound becomes. Below is an example of a square wave built from sine waves. As the file plays, more and more sine waves are added to increase the square-ness of the sound.
Here is an example of a sawtooth wave built in a similar way, but using both odd and even harmonics that descend proportionally in amplitude.
The sounds possible with additive techniques increase infinitely when you start to introduce inharmonic frequencies at various amplitudes and phases. Note what happens to this square wave built from sine waves when just some of the amplitudes of the natural harmonics are altered.
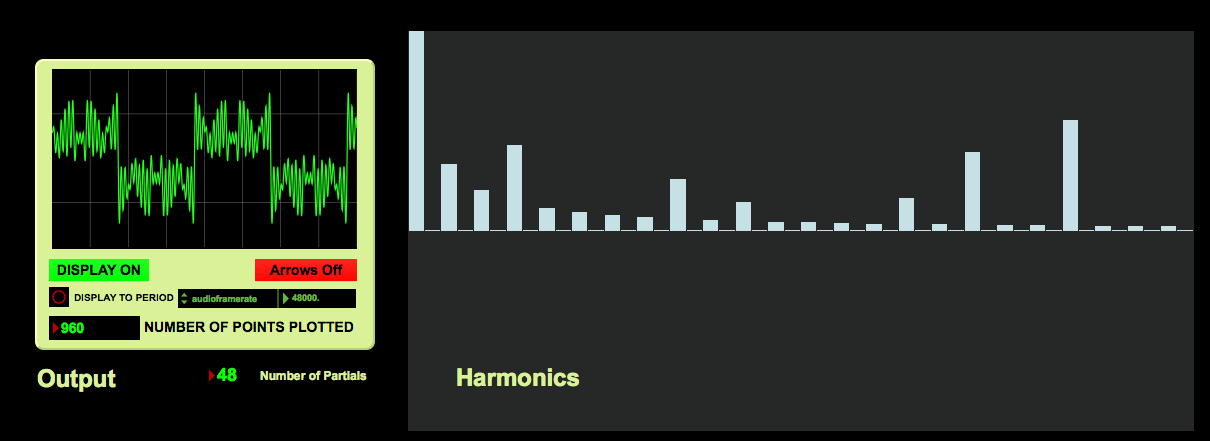
To get even more complex sounds, we can use Time-varying Additive Synthesis, in which “the mixture of sine waves varies over time…creating more interesting synthetic timbres and more realistic instrumental tones.” (Roads, 2012, p. 140)
If you can build more complex sounds with pure waveforms like sine waves, it stands to reason that given enough processing power and the right algorithms, we can analyze existing sounds and break them down into a collection of sine waves with varying attributes. FFT (or Fast Fourier Transform) methods are typically used for this purpose.
Once a sound is broken down into a table of data with numbers representing amplitude, frequency, phase and time, those numbers can be manipulated at will for a multitude of applications such as changing pitch without changing duration and vice versa, or visualizing sounds in a spectral display that allows graphic manipulation of the spectrum as in many waveform editors.
If there is a downside to additive synthesis it lies in the need for many, many oscillators and for the control data necessary in terms of frequency and amplitude envelopes. This is in stark contrast to other methods of synthesis such as FM or Subtractive Synthesis which are far more CPU friendly. Many virtual synthesizers use additive synthesis to some degree or combine the idea with other methods as in Logic Pro’s Alchemy.
Volumes have been written on Additive Synthesis and you should have no problem digging deeper if you so choose. To get familiar with other synthesis methods, control parameters, virtual and hardware instruments, etc., see the links below to my recent articles:
- Modular Synthesis
- Modulation and Control
- FabFilter Twin 2 Overview
- Synthesis Envelopes
- LFOs
- Granular Synthesis
- FM Synthesis
- iOS Synths
References
Roads, C.(2012). The Computer Music Tutorial. MIT Press.
Check out my other articles, reviews and interviews
Follow me on Twitter / Instagram / YouTube