Article Content

As mixing engineers, there are many tools available to process the sound of recorded audio signals. These tools are systems that take an input signal and produce a different output signal. We use many types of systems: acoustic, analog and digital.

With the use of computers, it’s possible to have sophisticated, powerful and complex digital systems. There are many advantages to digital systems, but also some limitations.

Modeling Systems

Digital systems can be used to model (i.e. simulate) acoustic and analog systems. This can be helpful if the necessary resources are not available to use the real acoustic or analog systems. As long as a computer is available, the modeled system can be duplicated and used.

The question then becomes: how accurate does the digital system model the acoustic or analog system?

Unfortunately, this cannot be answered simply. There are several categories of processors used in audio, many of which cannot be modeled in the same way.

Therefore, the accuracy of a model depends on the original system, its specific features and if the digital system recreates those features.

Modeling Linear, Time-Invariant Systems

There are many audio systems that are modeled as linear, time-invariant systems. If you’re not familiar with these technical terms, they’re not as difficult to understand as you might think.

A linear system processes signals with low amplitude identically to signals with high amplitude. An example is an equalizer that applies the same spectral curve to signals whether they’re quiet or loud.

A time-invariant system stays the same over time, and doesn’t change based on previous states of the system. An equalizer doesn’t change its spectral curve after you set the parameters.

Another way to understand time-invariant systems is to consider systems that are time-variant. Examples of audio systems that change are modulation effects (flanger, phaser, chorus etc.). Examples of audio systems that change based on previous states of the system are dynamic effects (compressors, expanders, think attack and release characteristics).

Impulse Response

An impulse response is a perfect representation of a linear, time-invariant system.

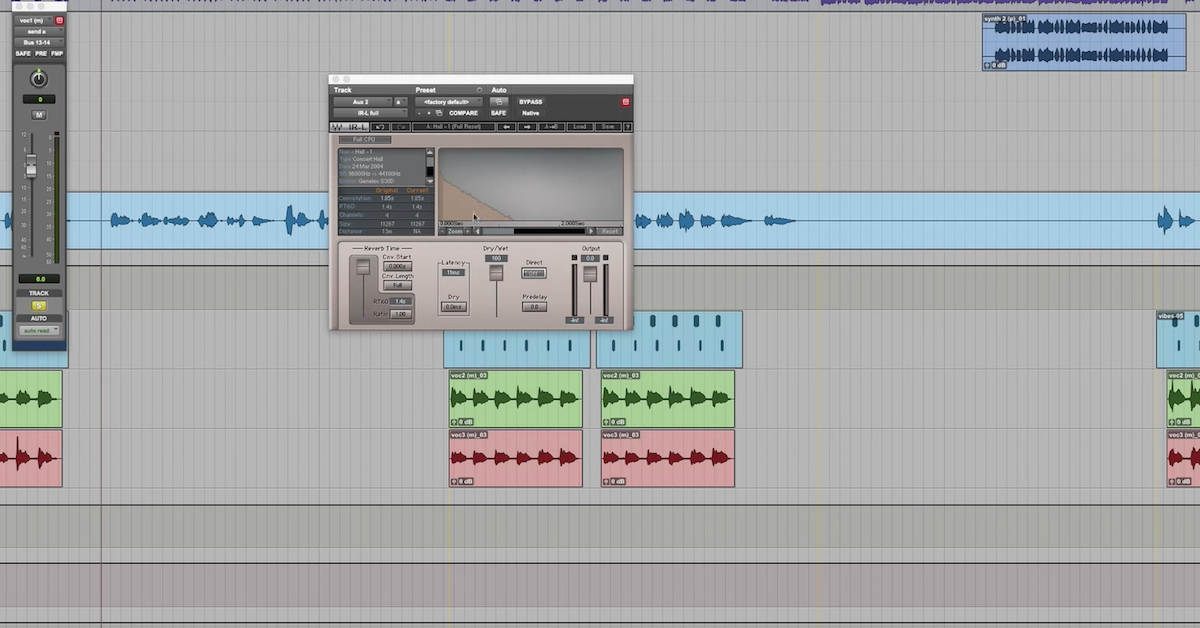
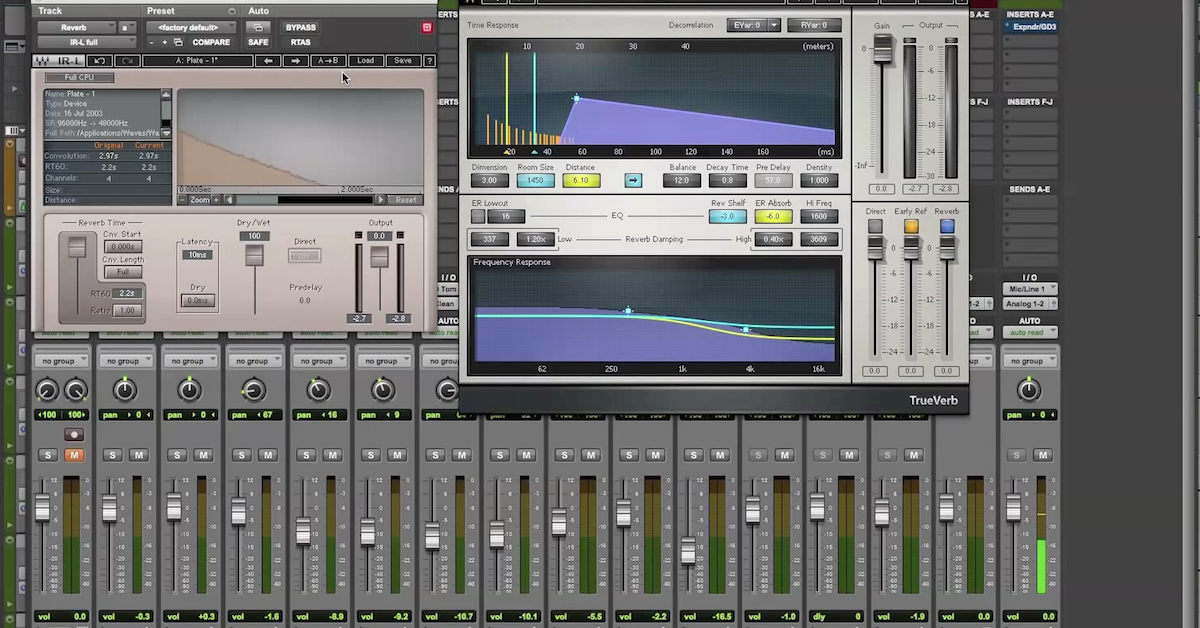
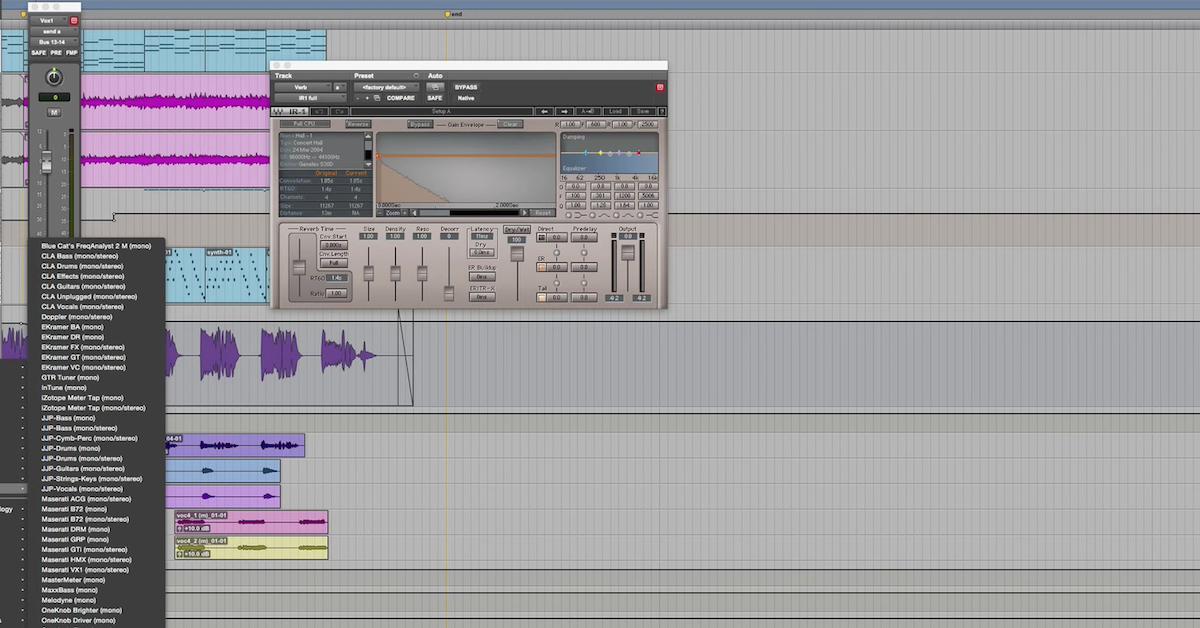
For digital systems, an IR represents how a single sample passes through the system. Digital signals are composed of a sequence of samples. To process the signal, each individual sample can be treated as creating its own impulse response. This sequence of impulse responses can be combined to create the processed signal – this is convolution.

Convolution is a mathematical operation that processes a signal with a system’s impulse response. The result of convolution represents the output of an acoustic or analog system.

If a system is linear and time-invariant, then the system’s impulse response is the optimal and mathematically perfect way to represent how a signal passes through the system. The limitation of convolution is that it cannot accurately represent how a signal is processed by a nonlinear or time-variant system.

So it really all comes down to determining whether or not acoustic and analog systems are linear, time-invariant (LTI) systems. If a particular system is LTI, convolution should be used. If not, convolution should not be used.

Case Study: Chamber Reverb

Convolution of an impulse response is a common method used to model the reverberation in an acoustic space. I had doubted that acoustic spaces were LTI systems, and therefore doubted that conventional, “static” convolution was a good way of representing these systems.

My motivation came from using sampled instrument libraries (drums, piano, etc.) that use multiple velocity layers and round-robins to improve realism. I thought that the same concept could be applied to impulse responses of acoustic spaces or guitar cabinets.

I wrote an algorithm for “dynamic convolution” that could convolve different IRs at many amplitude levels (addressing nonlinearity), and also could rotate between the “round-robins” at the same level (addressing time-variance).

Dynamic convolution is nothing new, it has been around for a while, and was patented several years ago.

Then I conducted an experiment (which I would welcome other people to replicate) to capture the impulses to be used by my algorithm. This experiment was conducted at Belmont University in Nashville, TN in the restored historic studio, Columbia Studio A. I used a full-range studio loudspeaker and Earthworks measurement microphone to capture IRs of the main studio space.

I recorded IRs at many different amplitude levels, starting at 96 dB SPL and decreasing in 6 dB increments until I reached the noise floor of the room (with all AC/ventilation shut off). I also recorded multiple IRs at each amplitude level (for the round-robins).

When I took the IRs back to the lab and started analyzing them, I was really surprised and really disappointed (in a good way).

After normalizing the amplitude of the IRs, there was no measurable difference between them. Even the quietest IR was similar to the loudest IR in all possible ways I could come up with to measure (correlation, RT-60, spectral response over time, etc).

This would suggest that acoustic spaces are LTI because the system has the same response to quiet signals and loud signals (linearity), and the system has the same response when measured over different times (time-invariant).

Therefore, I argue, conventional, “static” convolution with a room’s impulse response is an accurate method to represent an acoustic space.

---