Do We Really Need Another Article on the Decibel?
09/29/2015
Article Content
Last year I attended the Audio Engineering Society convention in Los Angeles. As I looked at the schedule of lectures and presentations, I rolled my eyes when I saw there were two one-hour lectures on the decibel.
Surely at a convention of audio engineers the information presented would be ground well covered by countless books and articles.
A few weeks later however I started thinking about the textbook definitions and even conversations with other engineers that showed there still is a bit of confusion about all this.
I then decided that yes, there does need to be one more article about the decibel.
The Definition (Really?)
In a computer programming course I took a few years ago we were studying the time it took for a program to complete its computations, which, depending on how it’s programmed, can be described with logarithms. In introducing the concepts, the teacher surprisingly told the class “I have a Ph.D. in computer science and a master’s degree in mathematics, but logarithms have always made me uncomfortable.” So when I first read the Yamaha Sound Reinforcement Handbook by Gary Davis and Ralph Jones and found myself confused by what seemed like a simple definition for what a decibel is, I figured there must be something they knew that I didn’t. The following is what confused me.
We start with the definition of the Bel, the logarithm of an electrical, acoustic, or other power ratio.
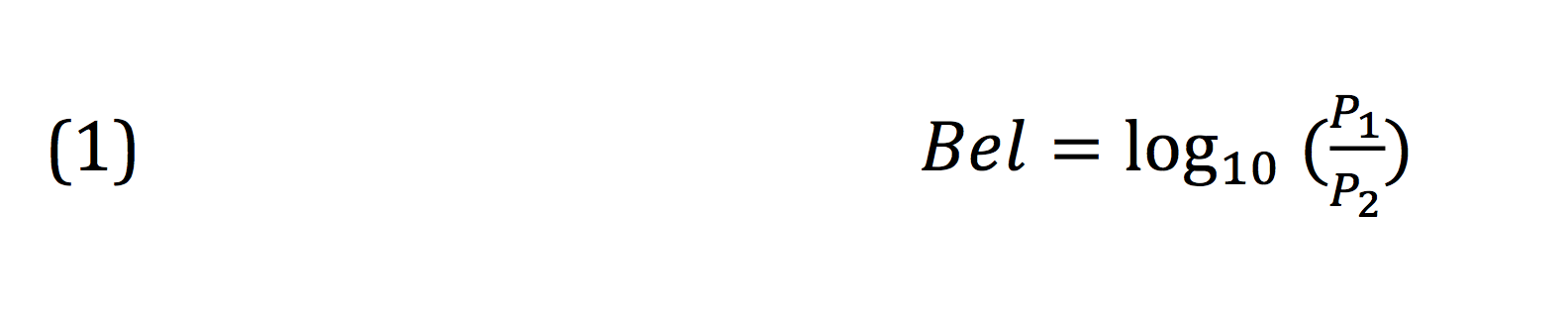
That seems straightforward, but now we want to define the decibel. The Yamaha Sound Reinforcement Handbook and, to be fair, many other engineering texts I’ve seen, define the decibel as below:
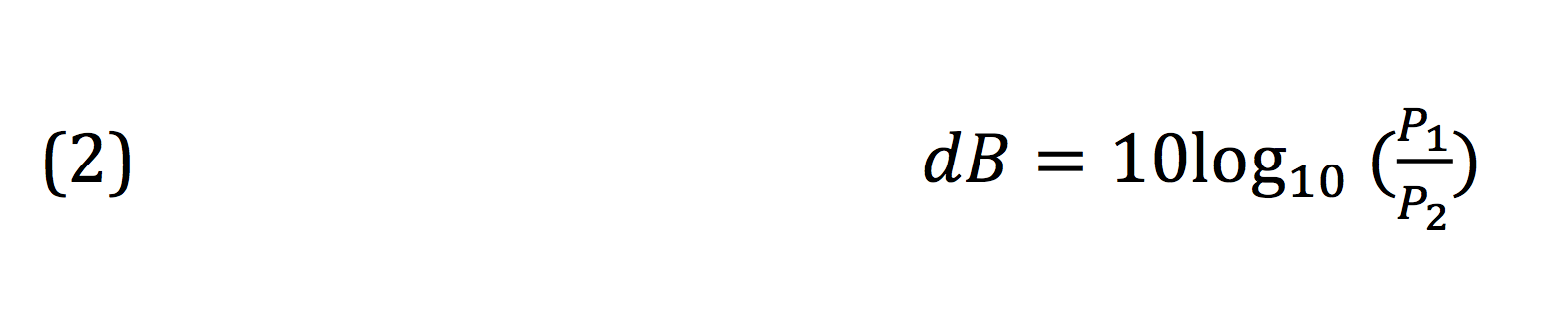
This looks very familiar, and we’ve all taken the above expression on faith. But when we look at it a bit more closely, does it hold up? The prefix “deci” means 1/10, so when we affix that term to the Bel on the left side of the first equation, we are dividing that term by 10. Those who have learned elementary algebra know that whatever one does to one side of an equation must be done to the other side for the expression to remain true. So if we divided the left side by 10, why do we multiply the right side by 10?
In what I believe is one of the worst statements I’ve ever read in a technical publication, the authors of the Sound Reinforcement Handbook state: “If you are not familiar with logs, it may not make much sense to you that the right half of the Bel equation is multiplied by 10 to get a value that’s supposed to be 1/10 of a Bel. This is correct, though.”
In one fell swoop, the authors offer an incorrect definition, then stiff-arm the confused reader by telling him or her to just accept it. In reality, almost every text shows the definition of dB this way, but that doesn’t mean it’s accurate or clear. So what’s the problem? Let’s start with the original definition of the Bel and work from there.
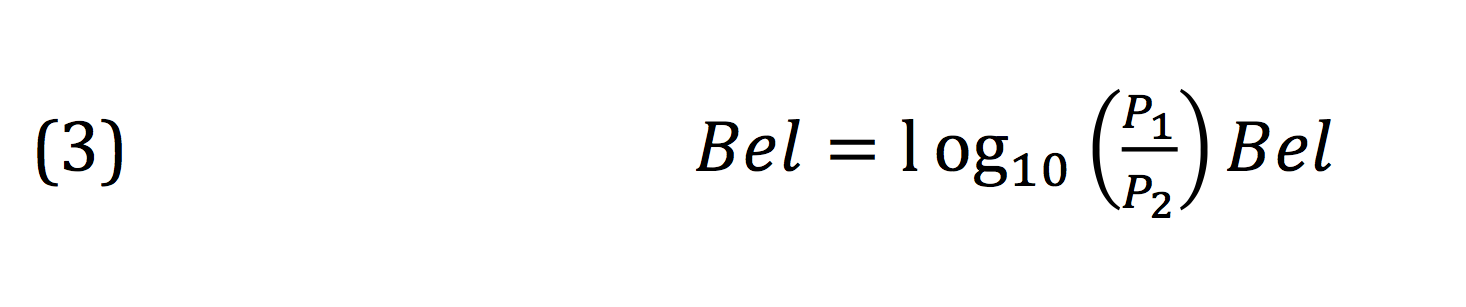Now, let’s divide just the right hand side by 10.
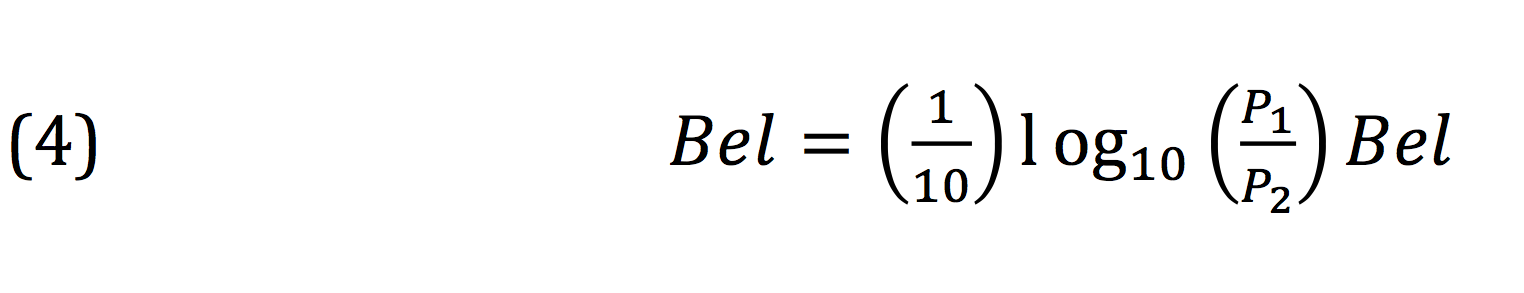But we know we can’t arbitrarily manipulate one side of the equation. We either have to perform the same operation on the other side, or neutralize our action. We divided the right hand side by 10, so let’s undo that by multiplying the right hand side by 10.
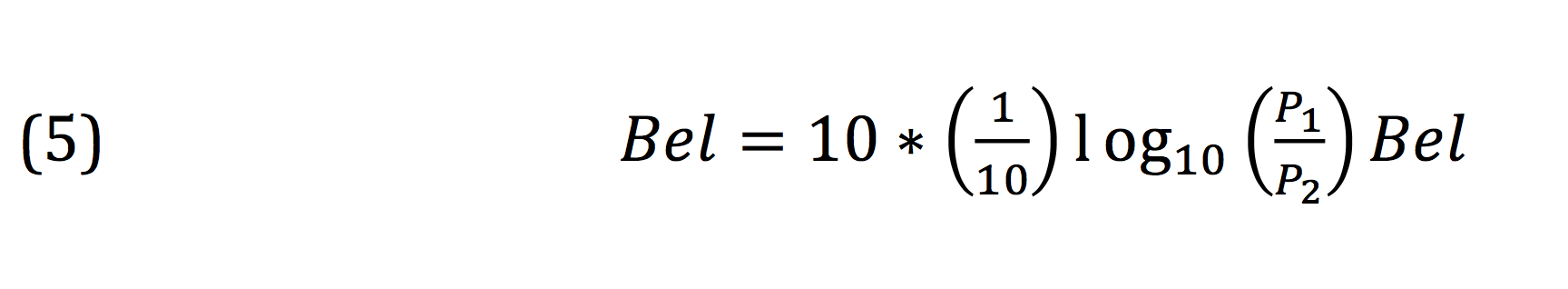Now, knowing that “deci” is the same as dividing by 10, let’s make that substitution.
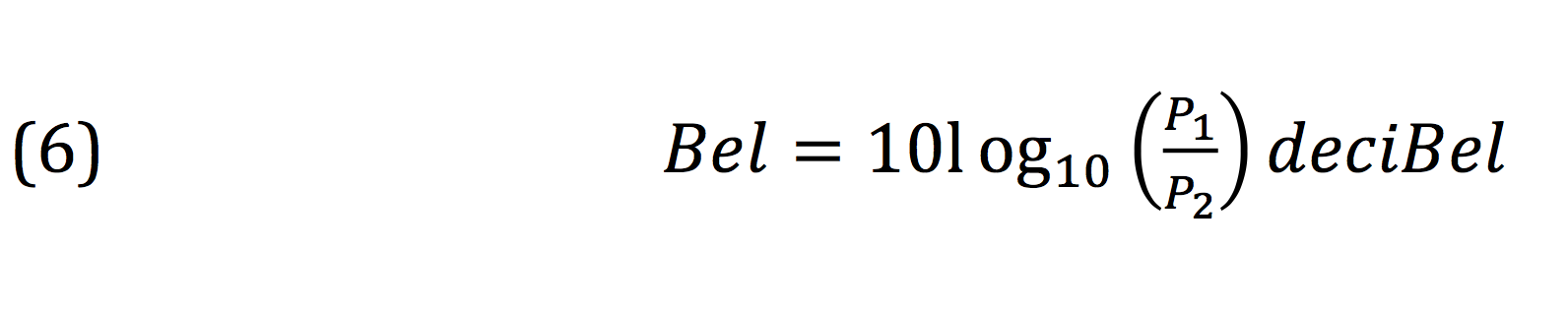The above expression is subtly but fundamentally different than that given in textbooks. The equation given in all of these texts comes from the fact that one can verbally define the decibel as 10 times the logarithm of the ratio of two power quantities. But when authors decide to format that statement as a pseudo-equation, which is what (1) is, the result is sloppy math and confusing writing.
So why do we even bother with the decibel? What was wrong with the Bel in the first place?
Scott Wilkinson, in his book Anatomy of a Home Studio, wrote “…Bels ‘compress’ power-ratio values too much to be useful in audio circuits. As a result, audio engineers use the decibel…”. Using Bels would almost always result in numerical values less than 10, often less than 1, in day-to-day calculations. Bumping the unit down by a factor of 10 let’s us increase the numbers by a factor of 10, and those numbers are then easier to deal with. In the end, it’s just about convenience.
Half: -3 dB or -6 dB?
Within my favorite DAW, Cubase, there’s a Gain function that all DAWs have. When you apply the process, a box appears in which you can type in by how many dB you want to increase or decrease your signal. What Cubase shows that most other audio software programs don’t is a raw scale factor displayed in percent. So, for instance, with a 0 dB adjustment, the scale factor is presented as 100%. This makes sense, as adjusting a signal by 0 dB, also known as unity, is the same as multiplying the signal by 1. When I enter a 6 dB reduction (actually 6.02 dB), Cubase tells me this will be a 50% reduction. In other words, the ratio of the output to the input of the process will be ½. Let’s put this into our dB formula.
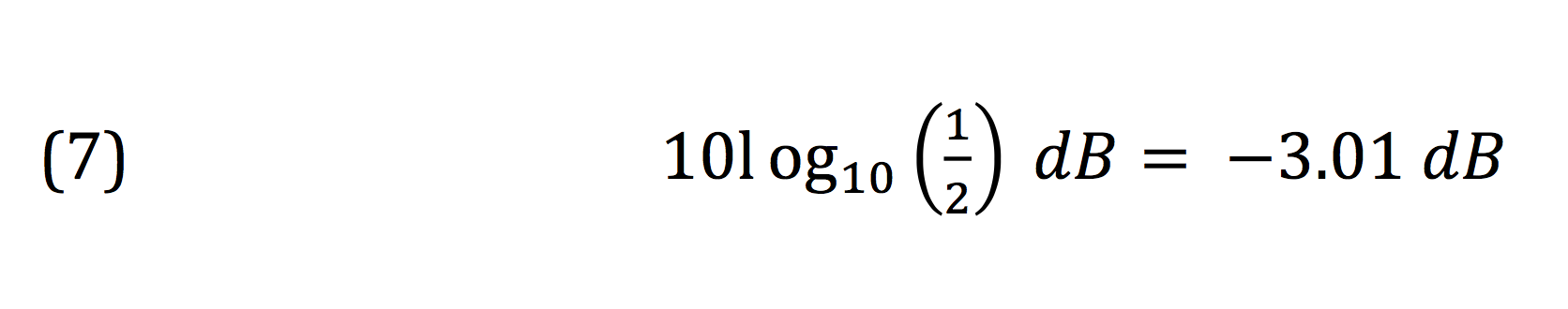Crap. Now what’s wrong? We went through all that trouble of meticulously defining the decibel, and now Cubase is telling us something’s up. By our calculation a 50% reduction in level should be a 3 dB drop, but Cubase is saying it’s 6 dB. The key to this apparent contradiction lies in one word in the definition of the decibel: power.
The decibel is a ratio of power levels. Power isn’t a property that can be directly measured, but is calculated using properties that can. In electrical engineering, voltage, amperage, and resistance are measured and can then be used to determine power used in a system.
Let’s take a look at how this is done, understanding that the digital samples in our DAW represent the analog voltages in an audio signal.
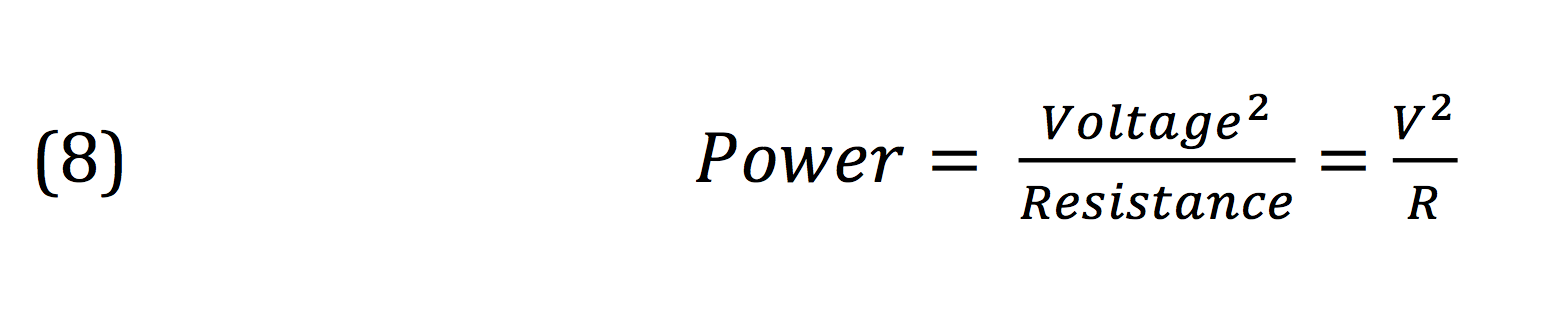For a gain function, we then have an input voltage Vin and an output voltage Vout. For the value of the resistance, we only have to mandate that the resistance is the same for both Vin and Vout. We can now plug (8) into (6):
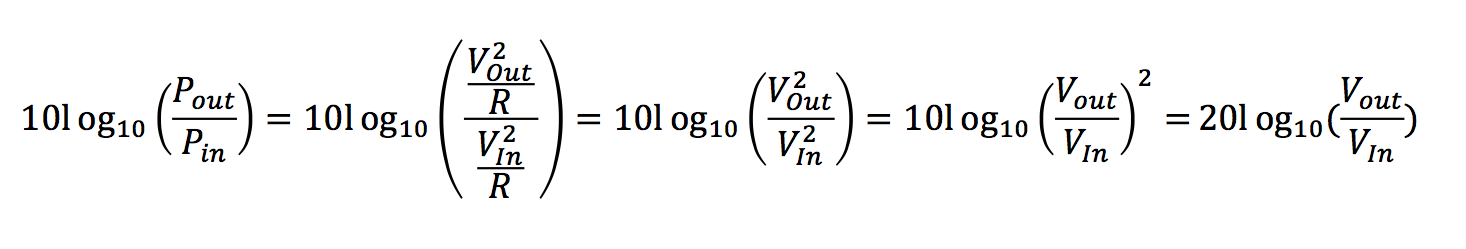We see that the resistance term, R, cancels out. The ratio of the square of the two voltage terms is the same as the ratio of the two voltage terms squared (read that while looking at the third and fourth terms in the series above). Lastly, by the property of logarithms, the value of any exponent of the argument (in this case, Vout/Vin) can be moved to the outside of the logarithm and used as a multiplier.
What this tells us is that when we’re dealing with voltage or current values in the analog domain or sample values in the digital domain, we have to use the multiplier 20 instead of 10 in order to use the decibel equation as it was intended: for power values. When we do, we see that all is right in the world and that Cubase was correct, of course.
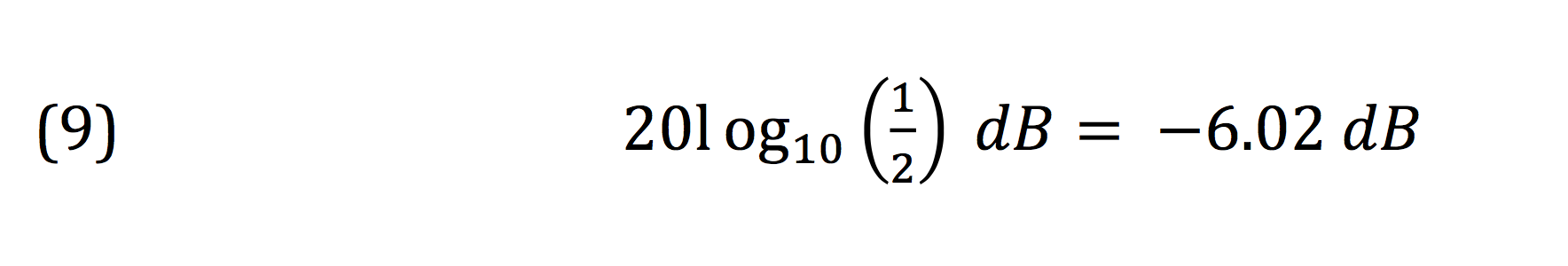Conclusion (aka So What?)
If you’re reading this section then you just finished a lengthy article on the definition of a term you’ve probably had no trouble using for years. Will what you know now make your mixes sound better? Probably not. Do you now have golden ears? Nope. Then why did I write this article? I wrote it because the decibel is a fundamental term in audio engineering, and having a deep understanding of it enables you to understand other concepts such as gain, power, signal flow, and more. Beyond this, the practice of learning terms and ideas at their most fundamental and basic level gives us the power to make better, more informed decisions. When we take information presented to us on faith, we give up our ability to discern fact from fiction. We let those with more opinions than sense, or those with an agenda, to dominate the studio, the lab, and online forums. As engineers, these concepts are our tools, and we should learn them inside and out.
Ready to elevate your ears?
It doesn’t have to take years to train your ears.
Get started today — and you’ll be amazed at how quickly using Quiztones for just a few minutes a day will improve your mixes, recordings, and productions!
Eleveate Your Ears
